Алгоритмы. Быстрая сортировка

Алгоритм быстрой сортировки является алгоритмом "разделяй и властвуй". Средняя сложность его выполнения O(n*log(n)), а вот в худших случаях O(n^2) и это "неочень".

Зачем же он нужен, если сортировка слиянием всегда имеет отличное O(n*log(n))?
Ответ простой: для его выполнения требуется значительно меньше дополнительной памяти - почти не требуется.

Пример, отсортируем массив [35,33,42,10,14,19,27,44,26,31].
Шаги выполнения:

Пример выполнения 2-го и 3-го шага

1. Проверим базовый случай (base case) - начало любого рекурсивного алгоритма. Для быстрой сортировки: если элементов в массиве 0 или 1, то его сортировать не нужно. Если элементов больше, то переходим к шагу 2.
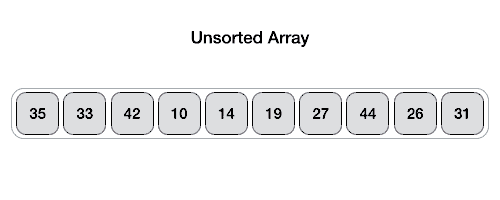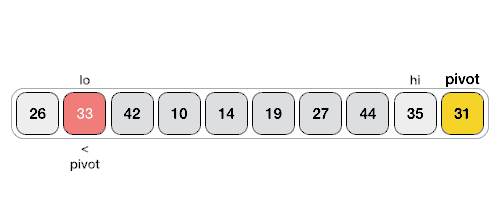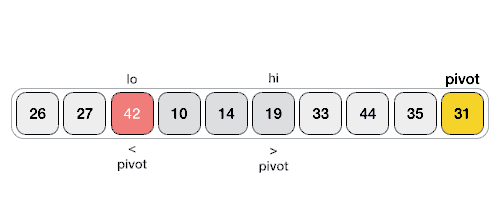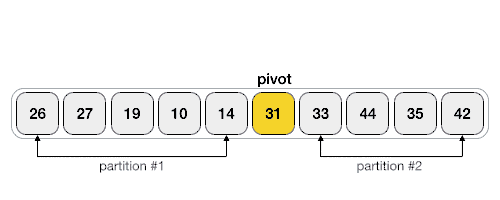
2. Выберем опорный элемент (pivot-элемент) в массиве. Это может быть любой элемент – первый, последний или случайный. Пусть в нашем случае опорным будет последний элемент - 31. 
3. Преобразуем массив. Относительно опорного q-элемента. Массив преобразуется следующим образом: [элементы <q, q, элементы >q]. Т.е. [26,27,19,10,14,31,33,44,35,42]
4. Рекурсивно выполним алгоритм на двух подмассивах - [l, q-1], [q+1, r]. Где l - это первый элемент, r - последний, q - опорный. 

В отличие от сортировки слиянием, основная логика этого алгоритма - выбор опорного элемента и преобразование массива, выполняется до дополнительных рекурсивных вызовов.

Сортируйте быстро, не сортируйте медленно.

Алгоритмы. Инверсии в массиве

Количество инверсий в массиве показывает, насколько это массив "хорошо" отсортирован. 

Что такое инверсия? Пара элементов A[i] и A[j] являются инверсией, если A[i] > A[j] и i < j. Массив [2, 4, 1, 3, 5] содержит три инверсии (2, 1), (4, 1), (4, 3). Максимальное количество инверсий в массиве из n элементов – (n*(n-1))/2.  Если в массиве инверсий нет, то массив полностью отсортирован. 

Зачем это считать? Например, вы решили узнать насколько у вас и вашей девушки схожие вкусы в выборе фильмов. Сделали список из 10 фильмов, которые и вы и она смотрели. Затем каждый для себя расположил эти фильмы в порядке от наиболее понравившегося к наименее. По одному из ваших списков отсортировали второй и посчитали количество инверсий. В итоге, если инверсии нет, то ваши вкусы идеально совпадают, а если их 45, то на вопрос "Что будем смотреть?", вы вряд ли найдёте быстрый ответ.

Как придумать название для приложения?

Практический пример. Придумаем, как назвать видеоредактор для айфона.

Начнём с того, что найдём и выпишем названия конкурентов. Это видеоредакторы: Quik, Splice и т.д.

Далее выберем 5 слов, которые лучше всего описывают наше приложение. Подойдут: video, editor, sounds, music, merge.

Для каждого слова в словарях, в разделах reverse dictionary, ищем 10-15 связанных слов и выписываем их. Например, jazz, disc, jam будут связанными с music.

Последний этап – генерация финального названия. Перебираем получившиеся слова и пытаемся два-три слова объединить в одно. Проверяем доступность доменного имени,  и, если всё ок, то регистрируем домен, и можно использовать название.

Результат

Словари:

http://www.onelook.com/
https://www.wordnik.com/
http://wikirhymer.com/

Генератор слов:

http://www.bustaname.com/

Проверка на доступность доменов и страниц:
https://namechk.com/
http://whois.domaintools.com/

Инструкция:

http://www.slideshare.net/purewest/howto-namethings/29-victorpineiro_amberhorsburghhttpubersuggestorg

Алгоритмы. Поиск подмассива максимальной суммы

Зачем искать подобный подмассив? Чтобы быть богатым и красивым. 

Пример. Известный астролог Павел Глоба по секрету рассказал вам об изменениях стоимости акций Apple. Следующие 16 дней их стоимость в долларах будет меняться так: [13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]. Это означает, например, что в первый день акции стали стоить на 13$ дороже, Наш искомый подмассив с максимальной суммой будет [18,20,-7,12], и она будет равна: 18+20+(-7)+12 = 43. Т.е. если вы купите акции в конце 7-ого дня (перед ростом в +18$), а затем продадите их в конце 11-го (перед паданием в -5$) вы заработаете 43$. Неплохие деньги.

Описание
Алгоритмы. Построение и анализ CLRS, Раздел 4.1 

Где жить во время путешествия?

Самые популярные ресурсы для поиска жилья это AirBnb и Booking. Booking - это про отели, AirBnb - про квартиры. На букинге отличный поиск по различным критериям, например, стоимость за ночь, возможность бесплатной отмены бронирования, тип жилья (отель или хостел), звёздность отеля и т.д. Плюс к этому есть карта с отелями. Возможности поиска на AirBnb ничуть не хуже. Тут можно заранее почитать отзывы о хозяине квартире. Выбирайте то, что вам больше нравится. Если нужна кухня, выбирайте AirBnb. Если дёшево и сердито, то Booking. 

A/B тестирование

AB-тесты – это прагматичный подход к тестированию нового функционала – когда функционал доступен только определенной группе людей, а не всем сразу. Вы делаете это для того, чтобы проверить готов ли ваш функционал и действительно ли он хорош, чтобы быть доступным всем. Пример, Instagram проверял реакцию людей на рекламу в ленте. Не все видели рекламу, но у тех, кто видел её, реакция оказалась очень негативной и Instagram отказался от это идеи (на тот момент). Facebook, Google, Instagram и другие компании постоянно используют AB-тесты, для проверки своих идей и гипотез. 

Инструменты для изучения английского языка

Если хотите увеличить словарный запас, то есть приложения Duolingo и LinguaLeo. Они содержат различные подходы к тренировке слов - аудирование, написание, перевод с русского на английский и наоборот и т.д. Чтобы лучше на слух воспринимать английскую речь, слушайте подкасты 6 Minutes от BBC Learning English, технические подкасты, например, Accidental Tech Podcast (ATP), или для вдохновления Entrepreneurial Thought Leaders. Также приятный способ изучения английского – это просмотр любимых сериалов, с субтитрами или без, например на ororo.tv. Есть много разных инструментов, но главное, чтобы вы понимали, зачем вам это нужно.

Аналитика мобильных приложений. Amplitude

Что пользователи делают в моём приложении? Сервис Amplitude поможет ответить на этот вопрос. Как он работает? На определенные действия в приложении вы отправляет на сервера Amplitude соотвествующие события. Например, на открытие экрана регистрации вы отправите "registration screen opened", а на успешную регистрацию "registration success". У вас есть цель, чтобы максимальный процент пользователей, которые попали на экран регистрации, успешно его прошли. Пример: в предыдущей версии приложения 60% пользователей прошли экран регистрации, затем вы сделали новый дизайн экрана и их количество упало до 45%. Вывод: нужно вернуть старый дизайн. Amplitude в свою очередь поможет найти такие критичные места в приложении.

amplitude.com